pyaibox.base package

Submodules

pyaibox.base.arrayops module

pyaibox.base.arrayops.arraycomb(arrays, out=None)

compute the elemnts combination of several lists.

Parameters

arrays (list or numpy array) – The lists or arrays.
out (numpy array, optional) – The combination results (defaults is None).

Returns

The combination results.

Return type

numpy array

Examples:

Compute the combination of three lists: \([1,2,3]\), \([4, 5]\), \([6,7]\), this will produce a \(12\times 3\) array.

x = arraycomb(([1, 2, 3], [4, 5], [6, 7]))
print(x, x.shape)

# output:
[[1 4 6]
[1 4 7]
[1 5 6]
[1 5 7]
[2 4 6]
[2 4 7]
[2 5 6]
[2 5 7]
[3 4 6]
[3 4 7]
[3 5 6]
[3 5 7]] (12, 3)

pyaibox.base.arrayops.cat(arrays, axis=None, out=None)

pyaibox.base.arrayops.cut(x, pos, axis=None)

Cut array at given position.

Parameters

x (numpy array) – an array to be cutted.
pos (tulpe or list) – cut positions: ((cpstart, cpend), (cpstart, cpend), …)
axis (int, tulpe or list, optional) – cut axis (the default is None, which means nothing)

pyaibox.base.arrayops.sl(dims, axis, idx=None)

slice any axis

generates slice of specified axis.

Parameters

dims (int) – total dimensions
axis (int or list) – select axis list.
idx (list or None, optional) – slice lists of the specified axis, if None, does nothing (the default)

Returns

slice for specified axis elements.

Return type

tuple of slice

Examples

import numpy as np

np.random.seed(2020)
X = np.random.randint(0, 100, (9, 10))
print(X, 'X)
print(X[sl(2, -1, [0, 1])], 'Xsl')

# output:

[[96  8 67 67 91  3 71 56 29 48]
[32 24 74  9 51 11 55 62 67 69]
[48 28 20  8 38 84 65  1 79 69]
[74 73 62 21 29 90  6 38 22 63]
[21 68  6 98  3 20 55  1 52  9]
[83 82 65 42 66 55 33 80 82 72]
[94 91 14 14 75  5 38 83 99 10]
[80 64 79 30 84 22 46 26 60 13]
[24 63 25 89  9 69 47 89 55 75]] X
[[96  8]
[32 24]
[48 28]
[74 73]
[21 68]
[83 82]
[94 91]
[80 64]
[24 63]] Xsl

pyaibox.base.baseops module

pyaibox.base.baseops.dmka(D, Ds)

Multi-key value assign

Parameters

D (dict) – main dict.
Ds (dict) – sub dict

pyaibox.base.baseops.dreplace(d, fv=None, rv='None', new=False)

pyaibox.base.baseops.redim(ndim, dim, cdim, keepcdim)

re-define dimensions

Parameters

ndim (int) – the number of dimensions
dim (int, tuple or list) – dimensions to be re-defined
cdim (int, optional) – If data is complex-valued but represented as real tensors, you should specify the dimension. Otherwise, set it to None, defaults is None. For example, \({\bm X}_c\in {\mathbb C}^{N\times C\times H\times W}\) is represented as a real-valued tensor \({\bm X}_r\in {\mathbb R}^{N\times C\times H\times W\ times 2}\), then cdim equals to -1 or 4.
keepcdim (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

Returns

re-defined dimensions

Return type

int, tuple or list

pyaibox.base.baseops.strfind(mainstr, patnstr)

find all patterns in string

Parameters

mainstr (str) – the main string
patnstr (str) – the pattern string

pyaibox.base.baseops.upkeys(D, mode='-', k='module.')

update keys of a dictionary

Parameters

D (dict) – the input dictionary
mode (str, optional) – '-' for remove key string which is specified by k, by default ‘-’ '+' for add key string which is specified by k, by default ‘-’
k (str, optional) – key string pattern, by default ‘module.’

Returns

new dictionary with keys updated

Return type

dict

pyaibox.base.mathops module

pyaibox.base.mathops.abs(X, caxis=None, keepaxis=False)

obtain amplitude of a array

Both complex and real representation are supported.

\[{\rm abs}({\bf X}) = |{\bf x}| = \sqrt{u^2 + v^2}, x\in {\bf X} \]

where, \(u, v\) are the real and imaginary part of x, respectively.

Parameters

X (array) – input
caxis (int or None) – If X is complex-valued, cdim is ignored. If X is real-valued and cdim is integer then X will be treated as complex-valued, in this case, cdim specifies the complex axis; otherwise (None), X will be treated as real-valued
keepaxis (bool, optional) – keep complex-dimension?

Returns

the inputs’s amplitude.

Return type

array

Examples

np.random.seed(2020)
X = np.random.rand(2, 3, 3)

print('---abs')
print(abs(X, caxis=0))
print(abs(X[0] + 1j * X[1]))

# ---output
---abs
[[0.99864747 0.88468226 0.91269439]
[0.78490066 0.48990863 0.40424448]
[0.72184896 0.40619981 1.02884318]]
[[0.99864747 0.88468226 0.91269439]
[0.78490066 0.48990863 0.40424448]
[0.72184896 0.40619981 1.02884318]]

pyaibox.base.mathops.c2r(X, caxis=-1, keepaxis=False)

convert complex-valued array to real-valued array

Parameters

X (numpy array) – input in complex representaion
caxis (int, optional) – complex axis for real-valued array. Defaults to -1.
keepaxis (bool, optional) – if False, stacks (make a new axis) at dimension cdim,

:param otherwise concatenates the real and imag part at exist dimension cdim: :type otherwise concatenates the real and imag part at exist dimension cdim: Default is False :param : :type : Default is False

Returns: output in real representaion
Return type: numpy array

see also r2c()

Examples

import numpy as np

np.random.seed(2020)

Xreal = np.random.randint(0, 30, (3, 2, 4))
Xcplx = r2c(Xreal, caxis=1)
Yreal = c2r(Xcplx, caxis=0, keepaxis=True)

print(Xreal, Xreal.shape, 'Xreal')
print(Xcplx, Xcplx.shape, 'Xcplx')
print(Yreal, Yreal.shape, 'Yreal')
print(np.sum(Yreal[0] - Xcplx.real), np.sum(Yreal[1] - Xcplx.imag), 'Error')

# output
[[[ 0  8  3 22]
[ 3 27 29  3]]

[[ 7 24 29 16]
[ 0 24 10  9]]

[[19 11 23 18]
[ 3  6  5 16]]] (3, 2, 4) Xreal

[[[ 0. +3.j  8.+27.j  3.+29.j 22. +3.j]]

[[ 7. +0.j 24.+24.j 29.+10.j 16. +9.j]]

[[19. +3.j 11. +6.j 23. +5.j 18.+16.j]]] (3, 1, 4) Xcplx

[[[[ 0.  8.  3. 22.]]

[[ 7. 24. 29. 16.]]

[[19. 11. 23. 18.]]]


[[[ 3. 27. 29.  3.]]

[[ 0. 24. 10.  9.]]

[[ 3.  6.  5. 16.]]]] (2, 3, 1, 4) Yreal

0.0 0.0, Error

pyaibox.base.mathops.conj(X, caxis=None)

conjugates a array

Both complex and real representation are supported.

Parameters

X (array) – input
caxis (int or None) – If X is complex-valued, cdim is ignored. If X is real-valued and cdim is integer then X will be treated as complex-valued, in this case, cdim specifies the complex axis; otherwise (None), X will be treated as real-valued

Returns

the inputs’s conjugate matrix.

Return type

array

Examples

np.random.seed(2020)
X = np.random.rand(2, 3, 3)

print('---conj')
print(conj(X, caxis=0))
print(conj(X[0] + 1j * X[1]))

# ---output
---conj
[[[ 0.98627683  0.87339195  0.50974552]
[ 0.27183571  0.33691873  0.21695427]
[ 0.27647714  0.34331559  0.86215894]]

[[-0.15669967 -0.14088724 -0.75708028]
[-0.73632492 -0.35566309 -0.34109302]
[-0.66680305 -0.21710064 -0.56142698]]]
[[0.98627683-0.15669967j 0.87339195-0.14088724j 0.50974552-0.75708028j]
[0.27183571-0.73632492j 0.33691873-0.35566309j 0.21695427-0.34109302j]
[0.27647714-0.66680305j 0.34331559-0.21710064j 0.86215894-0.56142698j]]

pyaibox.base.mathops.db2mag(db, s=20.0)

Converts decibel values to magnitudes

\[{\rm mag} = 10^{db / s} \]

Parameters

db (int, float, tuple, list, ndarray) – The decibel values.
s (int or float) – The scale value, default is 20.

Returns

The magnitudes of inputs with the same type.

Return type

int, float, tuple, list, ndarray

pyaibox.base.mathops.ebeo(a, b, op='+')

element by element operation

Element by element operation.

Parameters

a (list, tuple or ndarray) – The first list/tuple/ndarray.
b (list, tuple or ndarray) – The second list/tuple/ndarray.
op (str, optional) – Supported operations are: - '+' or 'add' for addition (default) - '-' or 'sub' for substraction - '*' or 'mul' for multiplication - '/' or 'div' for division - '**' or pow for power - '<', or 'lt' for less than - '<=', or 'le' for less than or equal to - '>', or 'gt' for greater than - '>=', or 'ge' for greater than or equal to - '&' for bitwise and - '|' for bitwise or - '^' for bitwise xor - function for custom operation.

Raises

TypeError – If the specified operator not in the above list, raise a TypeError.

pyaibox.base.mathops.ematmul(A, B, **kwargs)

Element-by-element complex multiplication

like A .* B in matlab

Parameters

A (array) – any size array, both complex and real representation are supported. For real representation, the real and imaginary dimension is specified by cdim or caxis.
B (array) – any size array, both complex and real representation are supported. For real representation, the real and imaginary dimension is specified by cdim or caxis.
cdim (int or None, optional) – if A and B are complex arrays but represented in real format, cdim or caxis should be specified (Default is None).

Returns

result of element-by-element complex multiplication with the same repesentation as A and B.

Return type

tensor

Examples

np.random.seed(2020)
Ar = np.random.randn(3, 3, 2)
Br = np.random.randn(3, 3, 2)

Ac = pb.r2c(Ar)
Bc = pb.r2c(Br)

Mr = pb.c2r(Ac * Bc)
print(np.sum(Mr - ematmul(Ar, Br, cdim=-1)))
print(np.sum(Ac * Bc - ematmul(Ac, Bc)))

# output
tensor(0)
tensor(0j)

pyaibox.base.mathops.fnab(n)

gives the closest two integer number factor of a number

Parameters

n (int or float) – the number

Returns

a (int)
b (int) – the factor number

Examples

print(fnab(5))
print(fnab(6))
print(fnab(7))
print(fnab(8))
print(fnab(9))

# ---output
(2, 3)
(2, 3)
(2, 4)
(2, 4)
(3, 3)

pyaibox.base.mathops.imag(X, caxis=None, keepaxis=False)

obtain imaginary part of a array

Both complex and real representation are supported.

Parameters

X (array) – input
caxis (int or None) – If X is complex-valued, cdim is ignored. If X is real-valued and cdim is integer then X will be treated as complex-valued, in this case, cdim specifies the complex axis; otherwise (None), X will be treated as real-valued
keepaxis (bool, optional) – keep complex-dimension?

Returns

the inputs’s imaginary part array.

Return type

array

Examples

np.random.seed(2020)
X = np.random.rand(2, 3, 3)

print('---imag')
print(imag(X, caxis=0))
print(imag(X[0] + 1j * X[1]))

# ---output
---imag
[[0.15669967 0.14088724 0.75708028]
[0.73632492 0.35566309 0.34109302]
[0.66680305 0.21710064 0.56142698]]
[[0.15669967 0.14088724 0.75708028]
[0.73632492 0.35566309 0.34109302]
[0.66680305 0.21710064 0.56142698]]

pyaibox.base.mathops.mag2db(mag, s=20.0)

Converts decibel values to magnitudes

\[{\rm db} = s*{\rm log10}{\rm mag} \]

Parameters

mag (int, float, tuple, list, ndarray) – The magnitude values.
s (int or float) – The scale value, default is 20.

Returns

The decibel of inputs with the same type.

Return type

int, float, tuple, list, ndarray

pyaibox.base.mathops.matmul(A, B, **kwargs)

Complex matrix multiplication

like A * B in matlab

Parameters

A (tensor) – any size tensor, both complex and real representation are supported. For real representation, the real and imaginary dimension is specified by cdim or caxis.
B (tensor) – any size tensor, both complex and real representation are supported. For real representation, the real and imaginary dimension is specified by cdim or caxis.
cdim (int or None, optional) – if A and B are complex tensors but represented in real format, cdim or caxis should be specified (Default is None).

Returns

result of complex multiplication with the same repesentation as A and B.

Return type

tensor

Examples

np.random.seed(2020)
Ar = np.random.randn(3, 3, 2)
Br = np.random.randn(3, 3, 2)

Ac = pb.r2c(Ar)
Bc = pb.r2c(Br)

print(np.sum(np.matmul(Ac, Bc) - matmul(Ac, Bc)))
Mr = matmul(Ar, Br, cdim=-1)
Mc = pb.c2r(np.matmul(Ac, Bc))
print(np.sum(Mr - Mc))

# output
tensor(0j)
tensor(0)

pyaibox.base.mathops.nextpow2(x)

get the next higher power of 2.

Given an number \(x\), returns the first p such that \(2^p >=|x|\).

Parameters: x (int or float) – an number.
Returns: Next higher power of 2.
Return type: int

Examples

print(prevpow2(-5), nextpow2(-5))
print(prevpow2(5), nextpow2(5))
print(prevpow2(0.3), nextpow2(0.3))
print(prevpow2(7.3), nextpow2(7.3))
print(prevpow2(-3.5), nextpow2(-3.5))

# output
2 3
2 3
-2 -1
2 3
1 2

pyaibox.base.mathops.pow(X, caxis=None, keepaxis=False)

obtain power of a array

Both complex and real representation are supported.

\[{\rm pow}({\bf X}) = |{\bf x}| = u^2 + v^2, x\in {\bf X} \]

where, \(u, v\) are the real and imaginary part of x, respectively.

Parameters

X (array) – input
caxis (int or None) – If X is complex-valued, cdim is ignored. If X is real-valued and cdim is integer then X will be treated as complex-valued, in this case, cdim specifies the complex axis; otherwise (None), X will be treated as real-valued
keepaxis (bool, optional) – keep complex-dimension?

Returns

the inputs’s power.

Return type

array

Examples

np.random.seed(2020)
X = np.random.rand(2, 3, 3)

print('---pow')
print(pow(X, caxis=0))
print(pow(X[0] + 1j * X[1]))

# ---output
---pow
[[0.99729677 0.78266271 0.83301105]
[0.61606904 0.24001046 0.1634136 ]
[0.52106592 0.16499828 1.05851829]]
[[0.99729677 0.78266271 0.83301105]
[0.61606904 0.24001046 0.1634136 ]
[0.52106592 0.16499828 1.05851829]]

pyaibox.base.mathops.prevpow2(x)

get the previous lower power of 2.

Given an number \(x\), returns the first p such that \(2^p <=|x|\).

Parameters: x (int or float) – an number.
Returns: Next higher power of 2.
Return type: int

Examples

print(prevpow2(-5), nextpow2(-5))
print(prevpow2(5), nextpow2(5))
print(prevpow2(0.3), nextpow2(0.3))
print(prevpow2(7.3), nextpow2(7.3))
print(prevpow2(-3.5), nextpow2(-3.5))

# output
2 3
2 3
-2 -1
2 3
1 2

pyaibox.base.mathops.r2c(X, caxis=-1, keepaxis=False)

convert real-valued array to complex-valued array

Convert real-valued array (the size of axis -th dimension is 2) to complex-valued array

Parameters

X (numpy array) – input in real representaion
caxis (int, optional) – the complex axis. Defaults to -1.
keepaxis (bool, optional) – if False, discards axis cdim,

:param otherwise preserves the axis cdim: :type otherwise preserves the axis cdim: Default is False :param : :type : Default is False :param (only work when the dimension at cdim equals 2):

Returns: complex-valued array
Return type: numpy array

Examples

import numpy as np

np.random.seed(2020)

Xreal = np.random.randint(0, 30, (3, 2, 4))
Xcplx = r2c(Xreal, caxis=1)
Yreal = c2r(Xcplx, caxis=0, keepaxis=True)

print(Xreal, Xreal.shape, 'Xreal')
print(Xcplx, Xcplx.shape, 'Xcplx')
print(Yreal, Yreal.shape, 'Yreal')
print(np.sum(Yreal[0] - Xcplx.real), np.sum(Yreal[1] - Xcplx.imag), 'Error')

# output
[[[ 0  8  3 22]
[ 3 27 29  3]]

[[ 7 24 29 16]
[ 0 24 10  9]]

[[19 11 23 18]
[ 3  6  5 16]]] (3, 2, 4) Xreal

[[[ 0. +3.j  8.+27.j  3.+29.j 22. +3.j]]

[[ 7. +0.j 24.+24.j 29.+10.j 16. +9.j]]

[[19. +3.j 11. +6.j 23. +5.j 18.+16.j]]] (3, 1, 4) Xcplx

[[[[ 0.  8.  3. 22.]]

[[ 7. 24. 29. 16.]]

[[19. 11. 23. 18.]]]


[[[ 3. 27. 29.  3.]]

[[ 0. 24. 10.  9.]]

[[ 3.  6.  5. 16.]]]] (2, 3, 1, 4) Yreal

0.0 0.0, Error

pyaibox.base.mathops.real(X, caxis=None, keepaxis=False)

obtain real part of a array

Both complex and real representation are supported.

Parameters

X (array) – input
caxis (int or None) – If X is complex-valued, cdim is ignored. If X is real-valued and cdim is integer then X will be treated as complex-valued, in this case, cdim specifies the complex axis; otherwise (None), X will be treated as real-valued
keepaxis (bool, optional) – keep complex-dimension?

Returns

the inputs’s real part array.

Return type

array

Examples

np.random.seed(2020)
X = np.random.rand(2, 3, 3)

print('---real')
print(real(X, caxis=0))
print(real(X[0] + 1j * X[1]))

# ---output
---real
[[0.98627683 0.87339195 0.50974552]
[0.27183571 0.33691873 0.21695427]
[0.27647714 0.34331559 0.86215894]]
[[0.98627683 0.87339195 0.50974552]
[0.27183571 0.33691873 0.21695427]
[0.27647714 0.34331559 0.86215894]]

pyaibox.base.randomfunc module

pyaibox.base.randomfunc.randgrid(start, stop, step, shake=0, n=None)

generates non-repeated uniform stepped random integers

Generates n non-repeated random integers from start to stop with step size step.

When step is 1 and shake is 0, it works similar to randperm,

Parameters

start (int or list) – start sampling point
stop (int or list) – stop sampling point
step (int or list) – sampling stepsize
shake (float) – the shake rate, if shake is 0, no shake, (default), if positive, add a positive shake, if negative, add a negative.
n (int or None) – the number of samples (default None, int((stop0 - start0) / step0) * int((stop1 - start1) / step1)…).

Return type

for multi-dimension, return a list of lists, for 1-dimension, return a list of numbers.

see randperm().

Example

Plot sampled randperm and randgrid point.

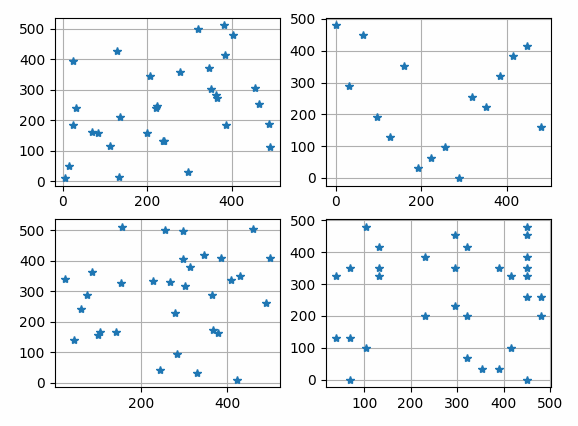
The results shown in the above figure can be obtained by the following codes.

import matplotlib.pyplot as plt

setseed(2021)
print(randperm(2, 40, 8), ", randperm(2, 40, 8)")
print(randgrid(2, 40, 1, -1., 8), ", randgrid(2, 40, 1, 8, -1.)")
print(randgrid(2, 40, 6, -1, 8), ", randgrid(2, 40, 6, 8)")
print(randgrid(2, 40, 6, 0.5, 8), ", randgrid(2, 40, 6, 8, 0.5)")
print(randgrid(2, 40, 6, -1, 12), ", randgrid(2, 40, 6, 12)")
print(randgrid(2, 40, 6, 0.5, 12), ", randgrid(2, 40, 6, 12, 0.5)")

mask = np.zeros((5, 6))
mask[3, 4] = 0
mask[2, 5] = 0

Rh, Rw = randperm2d(5, 6, 4, mask=mask)

print(Rh)
print(Rw)

N, H, W = 32, 512, 512

y1 = pb.randperm(0, H, N)
x1 = pb.randperm(0, W, N)
print(len(y1), len(x1))

y2 = pb.randgrid(0, H, 32, 0., N)
x2 = pb.randgrid(0, W, 32, 0., N)
print(len(y2), len(x2))
print(y2, x2)

y3, x3 = pb.randperm([0, 0], [H, W], N)
print(len(y3), len(x3))

y4, x4 = pb.randgrid([0, 0], [H, W], [32, 32], [0.25, 0.25], N)
print(len(y4), len(x4))

plt.figure()
plt.subplot(221)
plt.grid()
plt.plot(x1, y1, '*')
plt.subplot(222)
plt.grid()
plt.plot(x2, y2, '*')
plt.subplot(223)
plt.grid()
plt.plot(x3, y3, '*')
plt.subplot(224)
plt.grid()
plt.plot(x4, y4, '*')
plt.show()

pyaibox.base.randomfunc.randperm(start, stop, n)

randperm function like matlab

genarates diffrent random interges in range [start, stop)

Parameters

start (int or list) – start sampling point
stop (int or list) – stop sampling point
n (int, list or None) – the number of samples (default None, (stop - start))

Returns

P (list) – the randomly permuted intergers.
see randgrid(), randperm2d().

pyaibox.base.randomfunc.randperm2d(H, W, number, population=None, mask=None)

randperm 2d function

genarates diffrent random interges in range [start, end)

Parameters

H (int) – height
W (int) – width
number (int) – random numbers
population ({list or numpy array(1d or 2d)}) – part of population in range(0, H*W)

Returns

Ph (list) – the randomly permuted intergers in height direction.
Pw (list) – the randomly permuted intergers in width direction.

see randgrid(), randperm().

pyaibox.base.randomfunc.setseed(seed=None, target='numpy')

set seed

Set numpy / random seed.

Parameters

seed (int or None, optional) – seed for random number generator (the default is None)
target (str, optional) –
- 'numpy': np.random.seed(seed) (the default)
- 'random': random(seed)

pyaibox.base.typevalue module

pyaibox.base.typevalue.dtypes(t='int')

pyaibox.base.typevalue.peakvalue(A)

Compute the peak value of the input.

Find peak value in matrix

Parameters: A (numpy array) – Data for finding peak value
Returns: Peak value.
Return type: number

pyaibox.base package

Submodules

pyaibox.base.arrayops module

pyaibox.base.baseops module

pyaibox.base.mathops module

pyaibox.base.randomfunc module

pyaibox.base.typevalue module

Module contents