pyaibox.dsp package

Submodules

pyaibox.dsp.convolution module

pyaibox.dsp.convolution.conv1(f, g, shape='same', axis=0)

Convolution

The convoltuion between f and g can be expressed as

(1)\[\begin{aligned} (f*g)[n] &= \sum_{m=-\infty}^{+\infty}f[m]g[n-m] \\ &= \sum_{m=-\infty}^{+\infty}f[n-m]g[m] \end{aligned} \]
Parameters

  • f (numpy array) – data to be filtered, can be 2d matrix

  • g (numpy array) – convolution kernel

  • shape (int, optional) –

    • 'full': returns the full convolution,

    • 'same': returns the central part of the convolution

      that is the same size as x (default).

    • 'valid': returns only those parts of the convolution

      that are computed without the zero-padded edges. LENGTH(y)is MAX(LENGTH(x)-MAX(0,LENGTH(g)-1),0).

  • shape – convolution axis (the default is 0).

pyaibox.dsp.convolution.cutfftconv1(y, nfft, Nx, Nh, shape='same', axis=0, ftshift=False)

Throwaway boundary elements to get convolution results.

Throwaway boundary elements to get convolution results.

Parameters

  • y (numpy array) – array after iff.

  • nfft (int) – number of fft points.

  • Nx (int) – signal length

  • Nh (int) – filter length

  • shape (str) – output shape: 1. 'same' –> same size as input x, \(N_x\) 2. 'valid' –> valid convolution output 3. 'full' –> full convolution output, \(N_x+N_h-1\) (the default is ‘same’)

  • axis (int) – convolution axis (the default is 0)

  • ftshift (bool, optional) – whether to shift the frequencies (the default is False)

Returns

y – array with shape specified by same.

Return type

numpy array

pyaibox.dsp.convolution.fftconv1(x, h, shape='same', caxis=None, axis=0, keepcaxis=False, nfft=None, ftshift=False, eps=None)

Convolution using Fast Fourier Transformation

Convolution using Fast Fourier Transformation.

Parameters

  • x (numpy array) – data to be convolved.

  • h (numpy array) – filter array, it will be expanded to the same dimensions of x first.

  • shape (str, optional) – output shape: 1. 'same' –> same size as input x, \(N_x\) 2. 'valid' –> valid convolution output 3. 'full' –> full convolution output, \(N_x+N_h-1\) (the default is ‘same’)

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued.

  • axis (int, optional) – axis of convolution operation (the default is 0, which means the first dimension)

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued array and axis is not None but represents in real format. Default is False.

  • nfft (int, optional) – number of fft points (the default is \(2^{nextpow2(N_x+N_h-1)}\)), note that nfft can not be smaller than \(N_x+N_h-1\).

  • ftshift (bool, optional) – whether shift frequencies (the default is False)

  • eps (None or float, optional) – x[abs(x)<eps] = 0 (the default is None, does nothing)

Returns

y – Convolution result array.

Return type

numpy array

pyaibox.dsp.correlation module

pyaibox.dsp.correlation.accc(Sr, isplot=False)

Average cross correlation coefficient

Average cross correlation coefficient (ACCC)

\[\overline{C(\eta)}=\sum_{\eta} s^{*}(\eta) s(\eta+\Delta \eta) \]

where, \(\eta, \Delta \eta\) are azimuth time and it’s increment.

Parameters

Sr (numpy array) – SAR raw signal data \(N_a\times N_r\) or range compressed data.

Returns

ACCC in each range cell.

Return type

1d array

pyaibox.dsp.correlation.acorr(x, P, axis=0, scale=None)

computes auto-correlation using fft

Parameters

  • x (tensor) – the input signal array

  • P (int) – maxlag

  • axis (int) – the auto-correlation dimension

  • scale (str or None, optional) – None, 'biased' or 'unbiased', by default None

pyaibox.dsp.correlation.corr1(f, g, shape='same')

Correlation.

the correlation between f and g can be expressed as

(2)\[(f\star g)[n] = \sum_{m=-\infty}^{+\infty}{\overline{f[m]}g[m+n]} = \sum_{m=-\infty}^{+\infty}\overline{f[m-n]}g[m] \]
Parameters

  • f (numpy array) – data1

  • g (numpy array) – daat2

  • shape (str, optional) –

    • 'full': returns the full correlation,

    • 'same': returns the central part of the correlation

      that is the same size as f (default).

    • 'valid': returns only those parts of the correlation

      that are computed without the zero-padded edges. LENGTH(y)is MAX(LENGTH(f)-MAX(0,LENGTH(g)-1),0).

pyaibox.dsp.correlation.cutfftcorr1(y, nfft, Nx, Nh, shape='same', axis=0, ftshift=False)

Throwaway boundary elements to get correlation results.

Throwaway boundary elements to get correlation results.

Parameters

  • y (numpy array) – array after iff.

  • nfft (int) – number of fft points.

  • Nx (int) – signal length

  • Nh (int) – filter length

  • shape (str) – output shape: 1. 'same' –> same size as input x, \(N_x\) 2. 'valid' –> valid correlation output 3. 'full' –> full correlation output, \(N_x+N_h-1\) (the default is ‘same’)

  • axis (int) – correlation axis (the default is 0)

  • ftshift (bool, optional) – whether to shift the frequencies (the default is False)

Returns

y – array with shape specified by same.

Return type

numpy array

pyaibox.dsp.correlation.fftcorr1(x, h, shape='same', caxis=None, axis=0, keepcaxis=False, nfft=None, ftshift=False, eps=None)

Correlation using Fast Fourier Transformation

Correlation using Fast Fourier Transformation.

Parameters

  • x (numpy array) – data to be convolved.

  • h (numpy array) – filter array, it will be expanded to the same dimensions of x first.

  • shape (str, optional) – output shape: 1. 'same' –> same size as input x, \(N_x\) 2. 'valid' –> valid correlation output 3. 'full' –> full correlation output, \(N_x+N_h-1\) (the default is ‘same’)

  • caxis (int or None) – If x is complex-valued, caxis is ignored. If x is real-valued and caxis is integer then x will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), x will be treated as real-valued.

  • axis (int, optional) – axis of correlation operation (the default is 0, which means the first dimension)

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued array and axis is not None but represents in real format. Default is False.

  • nfft (int, optional) – number of fft points (the default is None, \(2^{nextpow2(N_x+N_h-1)}\)), note that nfft can not be smaller than \(N_x+N_h-1\).

  • ftshift (bool, optional) – whether shift frequencies (the default is False)

  • eps (None or float, optional) – x[abs(x)<eps] = 0 (the default is None, does nothing)

Returns

y – Correlation result array.

Return type

numpy array

pyaibox.dsp.correlation.xcorr(A, B, shape='same', mod=None, axis=0)

Cross-correlation function estimates.

Parameters

  • A (numpy array) – data1

  • B (numpy array) – data2

  • shape (str, optional) – output shape: 1. 'same' –> same size as input x, \(N_x\) 2. 'valid' –> valid correlation output 3. 'full' –> full correlation output, \(N_x+N_h-1\)

  • mod (str, optional) –

    • 'biased': scales the raw cross-correlation by 1/M.

    • 'unbiased': scales the raw correlation by 1/(M-abs(lags)).

    • 'coeff': normalizes the sequence so that the auto-correlations

      at zero lag are identically 1.0.

    • None: no scaling (this is the default).

pyaibox.dsp.ffts module

pyaibox.dsp.ffts.fft(x, n=None, norm=None, shift=False, **kwargs)

FFT in pyaibox

FFT in pyaibox, both real and complex valued tensors are supported.

Parameters

  • x (array) – When x is complex, it can be either in real-representation format or complex-representation format.

  • n (int, optional) – The number of fft points (the default is None –> equals to signal dimension)

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued.

  • axis (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued array and axis is not None but represents in real format. Default is False.

  • norm (None or str, optional) – Normalization mode. For the forward transform (fft()), these correspond to: - None - no normalization (default) - “ortho” - normalize by 1/sqrt(n) (making the FFT orthonormal)

  • shift (bool, optional) – shift the zero frequency to center (the default is False)

Returns

Examples

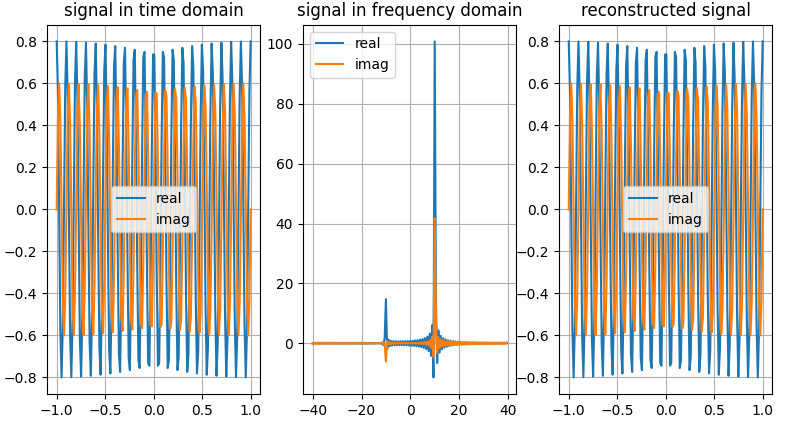
_images/FFTIFFTdemo.png

The results shown in the above figure can be obtained by the following codes.

import numpy as np
import pyaibox as pb
import matplotlib.pyplot as plt

shift = True
frq = [10, 10]
amp = [0.8, 0.6]
Fs = 80
Ts = 2.
Ns = int(Fs * Ts)

t = np.linspace(-Ts / 2., Ts / 2., Ns).reshape(Ns, 1)
f = pb.freq(Ns, Fs, shift=shift)
f = pb.fftfreq(Ns, Fs, norm=False, shift=shift)

# ---complex vector in real representation format
x = amp[0] * np.cos(2. * np.pi * frq[0] * t) + 1j * amp[1] * np.sin(2. * np.pi * frq[1] * t)

# ---do fft
Xc = pb.fft(x, n=Ns, caxis=None, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
xreal = pb.real(x, caxis=None, keepcaxis=False)
ximag = pb.imag(x, caxis=None, keepcaxis=False)
Xreal = pb.real(Xc, caxis=None, keepcaxis=False)
Ximag = pb.imag(Xc, caxis=None, keepcaxis=False)

# ---do ifft
x̂ = pb.ifft(Xc, n=Ns, caxis=None, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
x̂real = pb.real(x̂, caxis=None, keepcaxis=False)
x̂imag = pb.imag(x̂, caxis=None, keepcaxis=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()

# ---complex vector in real representation format
x = pb.c2r(x, caxis=-1)

# ---do fft
Xc = pb.fft(x, n=Ns, caxis=-1, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
xreal = pb.real(x, caxis=-1, keepcaxis=False)
ximag = pb.imag(x, caxis=-1, keepcaxis=False)
Xreal = pb.real(Xc, caxis=-1, keepcaxis=False)
Ximag = pb.imag(Xc, caxis=-1, keepcaxis=False)

# ---do ifft
x̂ = pb.ifft(Xc, n=Ns, caxis=-1, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
x̂real = pb.real(x̂, caxis=-1, keepcaxis=False)
x̂imag = pb.imag(x̂, caxis=-1, keepcaxis=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()
pyaibox.dsp.ffts.fft2(img)

Improved 2D fft

pyaibox.dsp.ffts.fftfreq(n, fs, norm=False, shift=False)

Return the Discrete Fourier Transform sample frequencies

Return the Discrete Fourier Transform sample frequencies.

Given a window length n and a sample rate fs, if shift is True:

f = [-n/2, ..., -1,     0, 1, ...,   n/2-1] / (d*n)   if n is even
f = [-(n-1)/2, ..., -1, 0, 1, ..., (n-1)/2] / (d*n)   if n is odd

Given a window length n and a sample rate fs, if shift is False:

f = [0, 1, ...,   n/2-1,     -n/2, ..., -1] / (d*n)   if n is even
f = [0, 1, ..., (n-1)/2, -(n-1)/2, ..., -1] / (d*n)   if n is odd

where \(d = 1/f_s\), if norm is True, \(d = 1\), else \(d = 1/f_s\).

Parameters

  • fs (float) – Sampling rate.

  • n (int) – Number of samples.

  • norm (bool) – Normalize the frequencies.

  • shift (bool) – Does shift the zero frequency to center.

Returns

frequency array with size \(n×1\).

Return type

numpy array

pyaibox.dsp.ffts.fftshift(x, **kwargs)

Shift the zero-frequency component to the center of the spectrum.

This function swaps half-spaces for all axes listed (defaults to all). Note that y[0] is the Nyquist component only if len(x) is even.

Parameters

  • x (numpy array) – The input array.

  • axis (int, optional) – Axes over which to shift. (Default is None, which shifts all axes.)

Returns

y – The shifted array.

Return type

numpy array

See also

ifftshift

The inverse of fftshift().

pyaibox.dsp.ffts.fftx(x, n=None)
pyaibox.dsp.ffts.ffty(x, n=None)
pyaibox.dsp.ffts.freq(n, fs, norm=False, shift=False)

Return the sample frequencies

Return the sample frequencies.

Given a window length n and a sample rate fs, if shift is True:

f = [-n/2, ..., n/2] / (d*n)

Given a window length n and a sample rate fs, if shift is False:

f = [0, 1, ..., n] / (d*n)

If norm is True, \(d = 1\), else \(d = 1/f_s\).

Parameters

  • n (int) – Number of samples.

  • fs (float) – Sampling rate.

  • norm (bool) – Normalize the frequencies.

  • shift (bool) – Does shift the zero frequency to center.

Returns

frequency array with size \(n×1\).

Return type

numpy array

pyaibox.dsp.ffts.ifft(x, n=None, norm=None, shift=False, **kwargs)

IFFT in pyaibox

IFFT in pyaibox, both real and complex valued tensors are supported.

Parameters

  • x (array) – When x is complex, it can be either in real-representation format or complex-representation format.

  • n (int, optional) – The number of ifft points (the default is None –> equals to signal dimension)

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued.

  • axis (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued array and axis is not None but represents in real format. Default is False.

  • norm (bool, optional) – Normalization mode. For the backward transform (ifft()), these correspond to: - None - no normalization (default) - “ortho” - normalize by 1``/sqrt(n)`` (making the IFFT orthonormal)

  • shift (bool, optional) – shift the zero frequency to center (the default is False)

Returns

pyaibox.dsp.ffts.ifftshift(x, **kwargs)

Shift the zero-frequency component back.

The inverse of fftshift(). Although identical for even-length x, the functions differ by one sample for odd-length x.

Parameters

  • x (numpy array) – The input array.

  • axis (int, optional) – Axes over which to shift. (Default is None, which shifts all axes.)

Returns

y – The shifted array.

Return type

numpy array

See also

fftshift

The inverse of ifftshift.

Examples

x = [1, 2, 3, 4, 5, 6]
y = np.fft.ifftshift(x)
print(y)
y = pb.ifftshift(x)
print(y)

x = [1, 2, 3, 4, 5, 6, 7]
y = np.fft.ifftshift(x)
print(y)
y = pb.ifftshift(x)
print(y)

axis = (0, 1)  # axis = 0, axis = 1
x = [[1, 2, 3, 4, 5, 6], [0, 2, 3, 4, 5, 6]]
y = np.fft.ifftshift(x, axis)
print(y)
y = pb.ifftshift(x, axis)
print(y)

x = [[1, 2, 3, 4, 5, 6, 7], [0, 2, 3, 4, 5, 6, 7]]
y = np.fft.ifftshift(x, axis)
print(y)
y = pb.ifftshift(x, axis)
print(y)
pyaibox.dsp.ffts.ifftx(x, n=None)
pyaibox.dsp.ffts.iffty(x, n=None)
pyaibox.dsp.ffts.padfft(X, nfft=None, axis=0, shift=False)

PADFT Pad array for doing FFT or IFFT

PADFT Pad array for doing FFT or IFFT

Parameters

  • X (ndarray) – Data to be padded.

  • nfft (int or None) – the number of fft point.

  • axis (int, optional) – Padding dimension. (the default is 0)

  • shift (bool, optional) – Whether to shift the frequency (the default is False)

pyaibox.dsp.frffts module

pyaibox.dsp.frffts.frfft(x, n=None, caxis=None, axis=0, keepcaxis=False, norm=None, shift=False)

Fractional FFT in pyaibox

Fractional FFT in pyaibox, both real and complex valued tensors are supported.

Parameters

  • x (array) – When x is complex, it can be either in real-representation format or complex-representation format.

  • n (int, optional) – The number of fft points (the default is None –> equals to signal dimension)

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued.

  • axis (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued array and axis is not None but represents in real format. Default is False.

  • norm (None or str, optional) – Normalization mode. For the forward transform (fft()), these correspond to: - None - no normalization (default) - “ortho” - normalize by 1/sqrt(n) (making the FFT orthonormal)

  • shift (bool, optional) – shift the zero frequency to center (the default is False)

Returns

  • y (array) – fft results array with the same type as x

  • see also ifft(), fftfreq(), freq().

Examples

_images/FFTIFFTdemo.png

The results shown in the above figure can be obtained by the following codes.

import numpy as np
import pyaibox as pb
import matplotlib.pyplot as plt

shift = True
frq = [10, 10]
amp = [0.8, 0.6]
Fs = 80
Ts = 2.
Ns = int(Fs * Ts)

t = np.linspace(-Ts / 2., Ts / 2., Ns).reshape(Ns, 1)
f = pb.freq(Ns, Fs, shift=shift)
f = pb.fftfreq(Ns, Fs, norm=False, shift=shift)

# ---complex vector in real representation format
x = amp[0] * np.cos(2. * np.pi * frq[0] * t) + 1j * amp[1] * np.sin(2. * np.pi * frq[1] * t)

# ---do fft
Xc = pb.fft(x, n=Ns, caxis=None, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
xreal = pb.real(x, caxis=None, keepcaxis=False)
ximag = pb.imag(x, caxis=None, keepcaxis=False)
Xreal = pb.real(Xc, caxis=None, keepcaxis=False)
Ximag = pb.imag(Xc, caxis=None, keepcaxis=False)

# ---do ifft
x̂ = pb.ifft(Xc, n=Ns, caxis=None, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
x̂real = pb.real(x̂, caxis=None, keepcaxis=False)
x̂imag = pb.imag(x̂, caxis=None, keepcaxis=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()

# ---complex vector in real representation format
x = pb.c2r(x, caxis=-1)

# ---do fft
Xc = pb.fft(x, n=Ns, caxis=-1, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
xreal = pb.real(x, caxis=-1, keepcaxis=False)
ximag = pb.imag(x, caxis=-1, keepcaxis=False)
Xreal = pb.real(Xc, caxis=-1, keepcaxis=False)
Ximag = pb.imag(Xc, caxis=-1, keepcaxis=False)

# ---do ifft
x̂ = pb.ifft(Xc, n=Ns, caxis=-1, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
x̂real = pb.real(x̂, caxis=-1, keepcaxis=False)
x̂imag = pb.imag(x̂, caxis=-1, keepcaxis=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()
pyaibox.dsp.frffts.frifft(x, n=None, caxis=None, axis=0, keepcaxis=False, norm=None, shift=False)

Fractional IFFT in pyaibox

Fractional IFFT in pyaibox, both real and complex valued tensors are supported.

Parameters

  • x (array) – When x is complex, it can be either in real-representation format or complex-representation format.

  • n (int, optional) – The number of fft points (the default is None –> equals to signal dimension)

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued.

  • axis (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued array and axis is not None but represents in real format. Default is False.

  • norm (None or str, optional) – Normalization mode. For the forward transform (fft()), these correspond to: - None - no normalization (default) - “ortho” - normalize by 1/sqrt(n) (making the FFT orthonormal)

  • shift (bool, optional) – shift the zero frequency to center (the default is False)

Returns

  • y (array) – fft results array with the same type as x

  • see also ifft(), fftfreq(), freq().

Examples

_images/FFTIFFTdemo.png

The results shown in the above figure can be obtained by the following codes.

import numpy as np
import pyaibox as pb
import matplotlib.pyplot as plt

shift = True
frq = [10, 10]
amp = [0.8, 0.6]
Fs = 80
Ts = 2.
Ns = int(Fs * Ts)

t = np.linspace(-Ts / 2., Ts / 2., Ns).reshape(Ns, 1)
f = pb.freq(Ns, Fs, shift=shift)
f = pb.fftfreq(Ns, Fs, norm=False, shift=shift)

# ---complex vector in real representation format
x = amp[0] * np.cos(2. * np.pi * frq[0] * t) + 1j * amp[1] * np.sin(2. * np.pi * frq[1] * t)

# ---do fft
Xc = pb.fft(x, n=Ns, caxis=None, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
xreal = pb.real(x, caxis=None, keepcaxis=False)
ximag = pb.imag(x, caxis=None, keepcaxis=False)
Xreal = pb.real(Xc, caxis=None, keepcaxis=False)
Ximag = pb.imag(Xc, caxis=None, keepcaxis=False)

# ---do ifft
x̂ = pb.ifft(Xc, n=Ns, caxis=None, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
x̂real = pb.real(x̂, caxis=None, keepcaxis=False)
x̂imag = pb.imag(x̂, caxis=None, keepcaxis=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()

# ---complex vector in real representation format
x = pb.c2r(x, caxis=-1)

# ---do fft
Xc = pb.fft(x, n=Ns, caxis=-1, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
xreal = pb.real(x, caxis=-1, keepcaxis=False)
ximag = pb.imag(x, caxis=-1, keepcaxis=False)
Xreal = pb.real(Xc, caxis=-1, keepcaxis=False)
Ximag = pb.imag(Xc, caxis=-1, keepcaxis=False)

# ---do ifft
x̂ = pb.ifft(Xc, n=Ns, caxis=-1, axis=0, keepcaxis=False, shift=shift)

# ~~~get real and imaginary part
x̂real = pb.real(x̂, caxis=-1, keepcaxis=False)
x̂imag = pb.imag(x̂, caxis=-1, keepcaxis=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()

pyaibox.dsp.function_base module

pyaibox.dsp.function_base.unwrap(x, discont=3.141592653589793, axis=-1)

Unwrap by changing deltas between values to \(2\pi\) complement.

Unwrap radian phase x by changing absoluted jumps greater than discont to their \(2\pi\) complement along the given axis.

Parameters

  • x (ndarray) – The input.

  • discont (float, optional) – Maximum discontinuity between values, default is \(\pi\).

  • axis (int, optional) – Axis along which unwrap will operate, default is the last axis.

Returns

The unwrapped.

Return type

ndarray

Examples

x = np.array([3.14, -3.12, 3.12, 3.13, -3.11])
y_np = unwrap(x)
print(y_np, y_np.shape, type(y_np))

# output

tensor([3.1400, 3.1632, 3.1200, 3.1300, 3.1732], dtype=torch.float64) torch.Size([5]) <class 'torch.Tensor'>
pyaibox.dsp.function_base.unwrap2(x, discont=3.141592653589793, axis=-1)

Unwrap by changing deltas between values to \(2\pi\) complement.

Unwrap radian phase x by changing absoluted jumps greater than discont to their \(2\pi\) complement along the given axis. The elements are divided into 2 parts (with equal length) along the given axis. The first part is unwrapped in inverse order, while the second part is unwrapped in normal order.

Parameters

  • x (Tensor) – The input.

  • discont (float, optional) – Maximum discontinuity between values, default is \(\pi\).

  • axis (int, optional) – Axis along which unwrap will operate, default is the last axis.

Returns

  • Tensor – The unwrapped.

  • see unwrap()

Examples

x = np.array([3.14, -3.12, 3.12, 3.13, -3.11])
y = unwrap(x)
print(y, y.shape, type(y))

print("------------------------")
x = np.array([3.14, -3.12, 3.12, 3.13, -3.11])
x = np.concatenate((x[::-1], x), axis=0)
print(x)
y = unwrap2(x)
print(y, y.shape, type(y))

# output
[3.14       3.16318531 3.12       3.13       3.17318531] (5,) <class 'numpy.ndarray'>
------------------------
[3.17318531 3.13       3.12       3.16318531 3.14       3.14
3.16318531 3.12       3.13       3.17318531] (10,) <class 'numpy.ndarray'>

pyaibox.dsp.interpolation1d module

pyaibox.dsp.interpolation1d.interp(x, xp, yp, mod='sinc')

interpolation

interpolation

Parameters

  • x (array_like) – The x-coordinates of the interpolated values.

  • xp (1-D sequence of floats) – The x-coordinates of the data points, must be increasing if argument period is not specified. Otherwise, xp is internally sorted after normalizing the periodic boundaries with xp = xp % period.

  • yp (1-D sequence of float or complex) – The y-coordinates of the data points, same length as xp.

  • mod (str, optional) – 'sinc' : sinc interpolation (the default is ‘sinc’)

Returns

y – The interpolated values, same shape as x.

Return type

float or complex (corresponding to fp) or ndarray

pyaibox.dsp.interpolation1d.sinc(x)
pyaibox.dsp.interpolation1d.sinc_interp(xin, r=1.0)
pyaibox.dsp.interpolation1d.sinc_table(Nq, Ns)

pyaibox.dsp.interpolation2d module

pyaibox.dsp.interpolation2d.interp2d(X, ratio=(2, 2), axis=(0, 1), method='cubic')

pyaibox.dsp.normalsignals module

pyaibox.dsp.normalsignals.chirp(t, T, Kr)

Create a chirp signal:

\[S_{tx}(t) = rect(t/T) * exp(1j*pi*Kr*t^2) \]
pyaibox.dsp.normalsignals.hs(x)

Heavyside function :

\[hv(x) = {1, if x>=0; 0, otherwise} \]
pyaibox.dsp.normalsignals.ihs(x)

Inverse Heavyside function:

\[ihv(x) = {0, if x>=0; 1, otherwise} \]
pyaibox.dsp.normalsignals.rect(x)

Rectangle function:

\[rect(x) = {1, if |x|<= 0.5; 0, otherwise} \]

Module contents